2022 MAA AMC 10A
- What is the value of the below expression?
问下式的值是多少?
\[ 3 + \frac{1}{3 + \frac{1}{3 + \frac{1}{3}}} \]
(A) \( \frac{31}{10} \)
(B) \( \frac{49}{15} \)
(C) \( \frac{33}{10} \)
(D) \( \frac{109}{33} \)
(E) \( \frac{15}{4} \)
(F) Leave as blank | 不作答
- Mike cycled 15 laps in 57 minutes. Assume he cycled at a constant speed throughout. Approximately how many laps did he complete in the first 27 minutes?
- The sum of three numbers is 96 . The first number is 6 times the third number, and the third number is 40 less than the second number. What is the absolute value of the difference between the first and second numbers?
- In some countries, automobile fuel efficiency is measured in liters per 100 kilometers while other countries use miles per gallon. Suppose that 1 kilometer equals \( m \) miles, and 1 gallon equals \( \ell \) liters. Which of the following gives the fuel efficiency in liters per 100 kilometers for a car that gets \( x \) miles per gallon?
- Square \( {ABCD} \) has side length 1. Points \( P, Q, R \) , and \( S \) each lie on a side of \( {ABCD} \) so that \( {APQCRS} \) is an equilateral convex hexagon with side length s. What is \( s \) ?
- Which expression is equal to \( \left| {a - 2 - \sqrt{{\left( a - 1\right) }^{2}}}\right| \) for \( a < 0 \) ?
- The least common multiple of a positive integer \( n \) and 18 is 180, and the greatest common divisor of \( n \) and 45 is 15 . What is the sum of the digits of \( n \) ?
- A data set consists of 6 (not distinct) positive integers:1,7,5,2,5, and \( X \) . The average (arithmetic mean) of the 6 numbers equals a value in the data set. What is the sum of all possible values of \( X \) ?
- A rectangle is partitioned into 5 regions as shown. Each region is to be painted a solid color-red, orange, yellow, blue, or green-so that regions that touch are painted different colors, and colors can be used more than once. How many different colorings are possible?
- Daniel finds a rectangular index card and measures its diagonal to be 8 centimeters. Daniel then cuts out equal squares of side \( 1\mathrm{\;{cm}} \) at two opposite corners of the index card and measures the distance between the two closest vertices of these squares to be \( 4\sqrt{2} \) centimeters, as shown below. What is the area of the original index card?
- Ted mistakenly wrote \( {2}^{m} \cdot \sqrt{\frac{1}{4096}} \) as \( 2 \cdot \sqrt[m]{\frac{1}{4096}} \) . What is the sum of all real numbers \( m \) for which these two expressions have the same value?
- On Halloween 31 children walked into the principal's office asking for candy. They can be classified into three types: Some always lie; some always tell the truth; and some alternately lie and tell the truth. The alternaters arbitrarily choose their first response, either a lie or the truth, but each subsequent statement has the opposite truth value from its predecessor. The principal asked everyone the same three questions in this order.
- Let \( \bigtriangleup {ABC} \) be a scalene triangle. Point \( P \) lies on \( \overline{BC} \) so that \( \overline{AP} \) bisects \( \angle {BAC} \) . The line through \( B \) perpendicular to \( \overline{AP} \) intersects the line through \( A \) parallel to \( \overline{BC} \) at point \( D \) . Suppose \( {BP} = 2 \) and \( {PC} = 3 \) . What is \( {AD} \) ?
- How many ways are there to split the integers 1 through 14 into 7 pairs so that in each pair the greater number is at least 2 times the lesser number?
- Quadrilateral \( {ABCD} \) with side lengths \( {AB} = 7,{BC} = {24},{CD} = {20} \) , and \( {DA} = {15} \) is inscribed in a circle. The area interior to the circle but exterior to the quadrilateral can be written in the form \( \frac{{a\pi } - b}{c} \) , where \( a, b \) , and \( c \) are positive integers such that \( a \) and \( c \) have no common prime factor. What is \( a + b + c \) ?
- The roots of the polynomial \( {10}{x}^{3} - {39}{x}^{2} + {29x} - 6 \) are the height, length, and width of a rectangular box (right rectangular prism). A new rectangular box is formed by lengthening each edge of the original box by 2 units. What is the volume of the new box?
- How many three-digit positive integers \( \underline{a}\underline{b}\underline{c} \) are there whose nonzero digits \( a, b \) , and \( c \) satisfy
Mike 用 57 分钟骑了 15 圈. 假设他一直以恒定的速度骑行. 那么他在前 27 分钟大约完成了多少圈?
(A) 5
(B) 7
(C) 9
(D) 11
(E) 13
(F) Leave as blank | 不作答
2022 MAA AMC 10A
三个数之和为 96 . 第一个数是第三个数的 6 倍, 第三个数比第二个数少 40 . 问第一个数与第二个数之差的绝对值是多少?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
(F) Leave as blank | 不作答
衡量汽车的燃油效率,一些国家采用每 100 千米用油的升数,而其他国家则使用每加仑汽油行驶的英里数. 假设 1 千米等于 \( m \) 英里,1加仑等于 \( \ell \) 升. 如果一辆汽车每加仑汽油可行驶 \( x \) 英里,那么以下哪个选项给出了以每 100 千米用油升数来衡量的燃油效率?
(A) \( \frac{x}{{100}\ell m} \)
(B) \( \frac{x\ell m}{100} \)
(C) \( \frac{\ell m}{100x} \)
(D) \( \frac{100}{x\ell m} \)
(E) \( \frac{{100}\ell m}{x} \)
(F) Leave as blank | 不作答
2022 MAA AMC 10A
正方形 \( {ABCD} \) 的边长为 1 . 点 \( P\text{、}Q\text{、}R\text{、}S \) 各自位于 \( {ABCD} \) 的一条边上,使
得 \( {APQCRS} \) 是边长为 \( s \) 的等边凸六边形. 问 \( s \) 是多少?
(A) \( \frac{\sqrt{2}}{3} \)
(B) \( \frac{1}{2} \)
(C) \( 2 - \sqrt{2} \)
(D) \( 1 - \frac{\sqrt{2}}{4} \)
(E) \( \frac{2}{3} \)
(F) Leave as blank | 不作答
已知 \( a < 0 \) ,那么哪个表达式与 \( \left| {a - 2 - \sqrt{{\left( a - 1\right) }^{2}}}\right| \) 相等?
(A) \( 3 - {2a} \)
(B) \( 1 - a \)
(C) 1
(D) \( a + 1 \)
(E) 3
(F) Leave as blank | 不作答
正整数 \( n \) 与 18 的最小公倍数是 180,并且 \( n \) 与 45 的最大公约数是 15 . 那么 \( n \) 的各位数字之和是多少?
(A) 3
(B) 6
(C) 8
(D) 9
(E) 12
(F) Leave as blank | 不作答
2022 MAA AMC 10A
一个数据集由 6 个 (可以相同的) 正整数组成: 1、7、5、2、5、X. 6 个数的 (算术)平均值等于数据集中的某个数. 问 \( X \) 的所有可能值的总和是多少?
(A) 10
(B) 26
(C) 32
(D) 36
(E) 40
(F) Leave as blank | 不作答
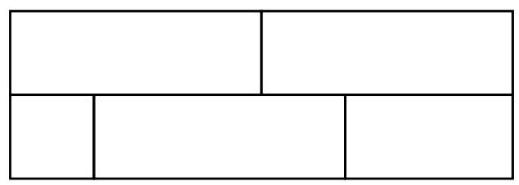
如图所示,一个矩形被划分为 5 个区域. 每个区域都将被用红色、橙色、黄色、蓝色或绿色中的一种颜色涂实,使得有接触的区域被涂上不同的颜色, 每种颜色可以使用多于一次. 问有多少种可能的染色方式?
(A) 120
(B) 270
(C) 360
(D) 540
(E) 720
(F) Leave as blank | 不作答
2022 MAA AMC 10A
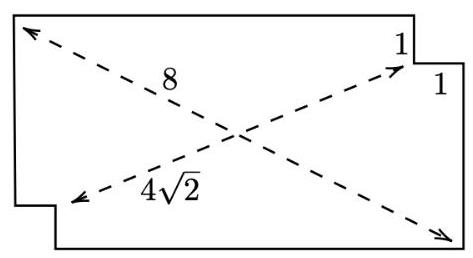
Daniel 找到了一张矩形索引卡片, 并测量出其对角线长为 8 厘米. Daniel 然后在索引卡片的两个对角处切出相同的边长为 1 厘米的正方形, 并测量出这两个正方形的两个最近的顶点之间的距离为 \( 4\sqrt{2} \) 厘米,如下图所示. 问原来索引卡片的面积是多少?
(A) 14
(B) \( {10}\sqrt{2} \)
(C) 16
(D) \( {12}\sqrt{2} \)
(E) 18
(F) Leave as blank | 不作答
Ted 错误地将 \( {2}^{m} \cdot \sqrt{\frac{1}{4096}} \) 写成 \( 2 \cdot \sqrt[m]{\frac{1}{4096}} \) . 问使得这两个表达式具有相同值的所有实数 \( m \) 的总和是多少?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
(F) Leave as blank | 不作答
2022 MAA AMC 10A
"Are you a truth-teller?"The principal gave a piece of candy to each of the 22 children who answered yes.
"Are you an alternater?"The principal gave a piece of candy to each of the 15 children who answered yes.
"Are you a liar?"The principal gave a piece of candy to each of the 9 children who answered yes.
How many pieces of candy in all did the principal give to the children who always tell the truth?
万圣节那天,31 个孩子走进校长办公室要糖果. 孩子们有三种类型:有些人总说谎话;有些人总说真话;有些人交替说谎话和真话. 对于那些交替说谎话和真话的孩子,每个人首先对自己的第一个回答做出是说谎话还是说真话的选择, 而随后的每次陈述是否说真话则与前一次情况相反. 校长按如下的顺序问了每个人同样的三个问题.
“你是总说真话吗?”校长给回答“是”的 22 个孩子每人一块糖果.
“你是交替说谎话和真话吗?”校长给回答“是”的 15 个孩子每人一块糖果.
“你是总说谎话吗?”校长给回答“是”的 9 个孩子每人一块糖果.
问校长给了总说真话的孩子们一共多少块糖果?
(A) 7
(B) 12
(C) 21
(D) 27
(E) 31
(F) Leave as blank | 不作答
2022 MAA AMC 10A
设 \( \bigtriangleup {ABC} \) 是三边不等的三角形. 点 \( P \) 在 \( \overline{BC} \) 上,使得 \( \overline{AP} \) 是 \( \angle {BAC} \) 的角平分线. 经过 \( B \) 的垂直于 \( \overline{AP} \) 的直线与经过 \( A \) 的平行于 \( \overline{BC} \) 的直线相交于点 \( D \) . 假设 \( {BP} = 2 \) 和 \( {PC} = 3 \) . 问 \( {AD} \) 的长度是多少?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
(F) Leave as blank | 不作答
将从 1 到 14 的整数分成 7 对, 使得每一对中较大的数至少是较小的数的 2 倍, 这样的分法一共有多少种?
(A) 108
(B) 120
(C) 126
(D) 132
(E) 144
(F) Leave as blank | 不作答
2022 MAA AMC 10A
圆内接四边形 \( {ABCD} \) 各边长为 \( {AB} = 7\text{、}{BC} = {24}\text{、}{CD} = {20}\text{、}{DA} = {15} \) . 在圆的内部但在四边形外部的区域的面积可以写成 \( \frac{{a\pi } - b}{c} \) 的形式,其中 \( a\text{、}b \) 、 \( c \) 是正整数,并且 \( a \) 和 \( c \) 没有共同的质因数. 问 \( a + \widetilde{b} + c \) 是多少?
(A) 260
(B) 855
(C) 1235
(D) 1565
(E) 1997
(F) Leave as blank | 不作答
多项式 \( {10}{x}^{3} - {39}{x}^{2} + {29x} - 6 \) 的根是一个长方体盒子 (底面是矩形的正棱柱) 的高度、长度和宽度. 如果一个新的长方体盒子是通过将原始盒子的每条边延长 2 个单位而形成. 问新盒子的体积是多少?
(A) \( \frac{24}{5} \)
(B) \( \frac{42}{5} \)
(C) \( \frac{81}{5} \)
(D) 30
(E) 48
(F) Leave as blank | 不作答
2022 MAA AMC 10A
\[ 0.\overline{\underline{a}\underline{b}\underline{c}} = \frac{1}{3}\left( {0.\bar{a} + 0.\bar{b} + 0.\bar{c}}\right) ? \]
(The bar indicates digit repetition; thus \( 0.\bar{a}\bar{b}\bar{c} \) is the infinite repeating decimal \( 0.\underline{a}\underline{b}\underline{c}\underline{a}\underline{b}\underline{c}\ldots \) )
三位正整数 \( \underline{a}\underline{b}\underline{c} \) 中的非零数字 \( a\text{、}b\text{、}c \) 满足
\[ 0.\overline{\underline{a}\underline{b}\underline{c}} = \frac{1}{3}\left( {0.\bar{a} + 0.\bar{b} + 0.\bar{c}}\right) , \]
(上划线表示数字循环;因此 \( 0.\bar{a}\bar{b}\bar{c} \) 是无限循环小数 \( 0.\bar{a}\bar{b}\bar{c}\bar{a}\bar{b}\bar{c}\ldots \) )问这样的整数有多少个?
(A) 9
(B) 10
(C) 11
(D) 13
(E) 14
(F) Leave as blank | 不作答
- Let \( {T}_{k} \) be the transformation of the coordinate plane that first rotates the plane \( k \) degrees counterclockwise around the origin and then reflects the plane across the \( y \) -axis. What is the least positive integer \( n \) such that performing the sequence of transformations \( {T}_{1},{T}_{2},{T}_{3},\cdots ,{T}_{n} \) returns the point (1,0)back to itself?
- Let \( {L}_{n} \) denote the least common multiple of the numbers \( 1,2,3,\ldots , n \) , and let \( h \) be the unique positive integer such that
设 \( {T}_{k} \) 为坐标平面的变换,它首先将平面绕原点逆时针旋转 \( k \) 度,然后再将平面沿 \( y \) 轴反射. 通过变换序列 \( {T}_{1}\text{、}{T}_{2}\text{、}{T}_{3}\text{、}\cdots \text{、}{T}_{n} \) 使得点(1,0)重新回到自身的最小正整数 \( n \) 是多少?
(A) 359
(B) 360
(C) 719
(D) 720
(E) 721
(F) Leave as blank | 不作答
2022 MAA AMC 10A
\[ \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{17} = \frac{h}{{L}_{17}}. \]
What is the remainder when \( h \) is divided by 17 ?
设 \( {L}_{n} \) 表示数 \( 1\text{、}2\text{、}3\text{、}\ldots \text{、}n \) 的最小公倍数,并设 \( h \) 是唯一的正整数,使得
\[ \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{17} = \frac{h}{{L}_{17}}. \]
问 \( h \) 除以 17 的余数是多少?
(A) 1
(B) 3
(C) 5
(D) 7
(E) 9
(F) Leave as blank | 不作答
- A four-term sequence is formed by adding each term of a four-term arithmetic sequence of positive integers to the corresponding term of a four-term geometric sequence of positive integers. The first three terms of the resulting four-term sequence are 57,60 , and 91 . What is the fourth term of this sequence?
- A bowl is formed by attaching four regular hexagons of side 1 to a square of side 1. The edges of adjacent hexagons coincide, as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons, situated on the rim of the bowl?
- Suppose that 13 cards numbered \( 1,2,3,\ldots ,{13} \) are arranged in a row. The task is to pick them up in numerically increasing order, working repeatedly from left to right. In the example below, cards 1, 2, 3 are picked up on the first pass, 4 and 5 on the second pass, 6 on the third pass, 7, 8, 9, 10 on the fourth pass, and 11, 12, 13 on the fifth pass.
- Isosceles trapezoid \( {ABCD} \) has parallel sides \( \overline{AD} \) and \( \overline{BC} \) , with \( {BC} < {AD} \) and \( {AB} = {CD} \) . There is a point \( P \) in the plane such that \( {PA} = 1,{PB} = 2,{PC} = 3 \) , and \( {PD} = 4 \) . What is \( \frac{BC}{AD} \) ?
- How many strings of length 5 formed from the digits0,1,2,3,4are there such that for each \( j \in \{ 1,2,3,4\} \) , at least \( j \) of the digits are less than \( j \) ? (For example, 02214 satisfies this condition because it contains at least 1 digit less than 1 , at least 2 digits less than 2 , at least 3 digits less than 3 , and at least 4 digits less than 4 . The string 23404 does not satisfy the condition because it does not contain at least 2 digits less than 2.)
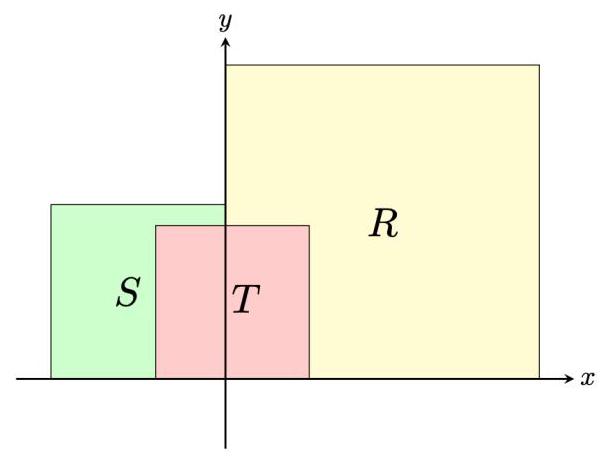
- Let \( R, S \) , and \( T \) be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the \( x \) -axis. The left edge of \( R \) and the right edge of \( S \) are on the \( y \) -axis, and \( R \) contains \( \frac{9}{4} \) as many lattice points as does \( S \) . The top two vertices of \( T \) are in \( R \cup S \) , and \( T \) contains \( \frac{1}{4} \) of the lattice points contained in \( R \cup S \) . See the figure below (not drawn to scale).
将一个由正整数组成的有四项的等差数列的每一项与一个由正整数组成的有四项的等比数列的对应项相加,得到一个四项数列. 由此形成的四项数列的前三项是 57、60、91. 问这个数列的第四项是多少?
(A) 190
(B) 194
(C) 198
(D) 202
(E) 206
(F) Leave as blank | 不作答
2022 MAA AMC 10A
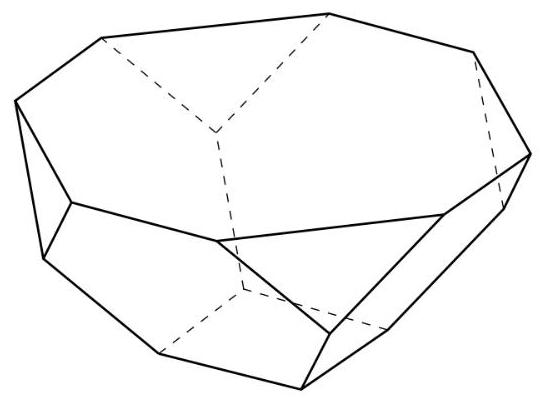
通过将四个边长为 1 的正六边形粘接到边长为 1 的正方形上形成一个碗. 如图所示,相邻的六边形有重合的边. 问位于碗的边缘,四个六边形最上方的八个顶点连接起来得到的八边形的面积是多少?
(A) 6
(B) 7
(C) \( 5 + 2\sqrt{2} \)
(D) 8
(E) 9
(F) Leave as blank | 不作答
2022 MAA AMC 10A
For how many of the 13! possible orderings of the cards will the 13 cards be picked up in exactly two passes?
假设编号为 1、2、3、...、13 的 13 张卡片排成一行. 现在的任务是按数值递增的顺序拾取它们, 从左到右重复工作. 在下面的示例中, 第一轮时拿起编号为 1、2、3 的卡片,第二轮时拿起编号为 4 和 5 的卡片,第三轮时拿起编号为 6 的卡片, 第四轮时拿起编号为 7、8、9、10 的卡片, 第五轮时拿起编号为 11、12、13 的卡片.
在所有 13! 种可能的卡片排列中, 有多少种排列使得 13 张卡片可通过恰好两轮被拾取?

(A) 4082
(B) 4095
(C) 4096
(D) 8178
(E) 8191
(F) Leave as blank | 不作答
2022 MAA AMC 10A
在等腰梯形 \( {ABCD} \) 中, \( \overline{AD} \) 和 \( \overline{BC} \) 是平行的两边, \( {BC} < {AD} \) ,并且 \( {AB} = {CD} \) . 平面上有一个点 \( P \) ,使得 \( {PA} = 1\text{、}{PB} = 2\text{、}{PC} = 3\text{、}{PD} = 4 \) . 问 \( \frac{BC}{AD} \) 是多少?
(A) \( \frac{1}{4} \)
(B) \( \frac{1}{3} \)
(C) \( \frac{1}{2} \)
(D) \( \frac{2}{3} \)
(E) \( \frac{3}{4} \)
(F) Leave as blank | 不作答
考虑由数字 0、1、2、3、4 组成的长度为 5 的字符串,满足对于每个 \( j \in \) \( \{ 1,2,3,4\} \) ,字符串中至少有 \( j \) 个小于 \( j \) 的数字,问这样的字符串有多少个? (例如, 02214 满足此条件, 因为它包含至少 1 个小于 1 的数字、至少 2 个小于 2 的数字、至少 3 个小于 3 的数字、至少 4 个小于 4 的数字. 字符串 23404 不满足条件, 因为它不包含至少 2 个小于 2 的数字.)
(A) 500
(B) 625
(C) 1089
(D) 1199
(E) 1296
(F) Leave as blank | 不作答
2022 MAA AMC 10A
The fraction of lattice points in \( S \) that are in \( S \cap T \) is 27 times the fraction of lattice points in \( R \) that are in \( R \cap T \) . What is the minimum possible value of the edge length of \( R \) plus the edge length of \( S \) plus the edge length of \( T \) ?
已知 \( R\text{、}S\text{、}T \) 是坐标平面上以格点(即横纵坐标均为整数的点)为顶点的正方形及其内部. 每个正方形的底边位于 \( x \) 轴上. \( R \) 的左边缘和 \( S \) 的右边缘在 \( y \) 轴上, \( R \) 中的格点数是 \( S \) 中的格点数的 \( \frac{9}{4} \) 倍. \( T \) 的上方的两个顶点在 \( R \cup S \) 中, \( T \) 中的格点数是 \( R \cup S \) 中的格点数的 \( \frac{1}{4} \) . 如下图所示 (未按比例绘制). \( S \cap T \) 中的格点在 \( S \) 中的格点所占比例是 \( R \cap T \) 中的格点在 \( R \) 中的格点所占比例的 27 倍. 问 \( R \) 的边长,加上 \( S \) 的边长,加上 \( T \) 的边长的最小可能值是多少?
(A) 336
(B) 337
(C) 338
(D) 339
(E) 340
(F) Leave as blank | 不作答
2022 MAA AMC 10A
Answers.
DBEEC ABDDE CACED DDACE BDBEB